Exercise 1.1 (Brightspace registrations)

1. To be able to hand in your assignments, your handin group (max 3 persons) has to be registered in Brightspace. Please ask your teaching assistant to register your group. Your group will be visible under "Course Tools > Groups".

2. (Optional) On the course webpage visit the "Activity Tools > Discussions", and subscribe to the different forums and topics to get notifications when there are new postings.

Exercise 1.2 (install Python)

Install the most recent version of Python 3 from python.org. See Installing Python in the course menu for more information.

Exercise 1.3 (shared folder) [optional]

Create a shared online folder for your exercise class ("TØ hold"), where you can share your solutions to the exercises presented during the exercise classes. Aarhus University provides OneDrive and Brightspace for this purpose.

Exercise 2.1 (sum of two numbers)

Create a program that asks the user for two numbers and then prints their sum.

Hint. Use the function input. Recall that the function input returns a str.

Exercise 2.2 (sum of k numbers)

Create a program that adds a user specified number of numbers. The program should first ask the user for a number k, and then k times ask the user for a number, and finally print the sum of the k numbers.

Hint. Use a while-loop.

Exercise 2.3 (intersection of two intervals)

Write a program that determines if two intervals [a, b] and [c, d] overlap, where a ≤ b and c ≤ d. The program should ask the user for the four end-points a, b, c and d of the two intervals, and print if the two intervals overlap or not. If the two intervals overlap, the program should print the interval where the two input intervals overlap.

Hint. Use one or more if-statements.

Examples:

[2, 4] and [6, 9] do not overlap
[5, 7] and [1, 3] do not overlap
[4, 8] and [-6, 2] do not overlap
[2, 5] and [3, 9] overlap in the interval [3, 5]
[3, 6] and [1, 3] overlap in the interval [3, 3]
[1, 8] and [2, 6] overlap in the interval [2, 6]

Exercise 2.4 (integer square root)

Consider the following program for finding the integer square root of a non-negative integer:

x = int(input('x: '))

low = 0
high = x + 1

while True:  # low <= sqrt(x) < high
    if low + 1 == high:
        break

    mid = (high + low) // 2

    if mid * mid <= x:
        low = mid
        continue

    high = mid

print(low)  # low = floor(sqrt(x))

1. Walk through and understand the program.

2. Try to simplify the program, getting rid of the break and continue statements.

Exercise 2.5 (primality test)

Write a naive program that tests if a small number x ≥ 2 is a prime number.

Recall that a number is a prime number if and only if the only numbers dividing the number is 1 and the number itself, like the numbers 2, 3, 5, 7, 11, 13...

The program should ask the user for the number x and print whether the number is a prime or not. If x is not a prime, it should print a divisor/factor in the range [2, x - 1].

Hint. Try all relevant factors. Use the % operator to compute the remainder by integer division, e.g. 13 % 5 == 3.

Exercise 2.6 (integer factorization)

Write a program that, given a positive integer x, prints the prime factors of that number. Recall that any positive number has a unique prime factorization, e.g. 126 = 2 * 3 * 3 * 7.

The program should ask the user for the integer x, and then print each prime factor. Note that for x = 126, the prime factor 3 should be printed two times.

Hint. Repeatedly divide x by 2 until 2 is not a prime factor any longer. Repeat the same for 3, 4, 5,... Note that 4 = 2 * 2 is not a prime number. But since its prime factors cannot be divisors of x divided by the prime factors found so far, then we will not find 4 (and any other composite number) as a prime divisor of x.

Exercise 2.7* (Newton-Raphson square root)

Use the Newton-Raphson method to compute the square root of a float n ≥ 1.0, by finding a root of the function f(x) = x² - n and letting your initial approximation of the root be x = n. Recall f'(x) = 2 * x. In your computations you can use +, -, *, and /.

You can compare your result to the result of the builtin sqrt function in the math module using:

import math
print(math.sqrt(n))

Exercise 2.8** (Stirlings's approximation)

Stirling's approximation states that n! can be approximated by S(n) = (2 π n)^0.5 · (n / e)ⁿ.

Write a program that asks the user for an n and prints the ratio n! / S(n), i.e. how good an approximation S(n) is to n!.

Some example outputs:

1! / S(1) = 1.08443755
10! / S(10) = 1.00836536
100! / S(100) = 1.00083368
1000! / S(1000) = 1.00008334
10000! / S(10000) = 1.00000833
100000! / S(100000) = 1.00000083

Note: Use import math to get access to the constants math.pi and math.e.

Warning: Computing the ratio for larger n can be tricky.

This exercise is inspired by a problem from Kattis.

Exercise 3.1 (text formatting)

Consider the below code. Run the code and explain the output.

from math import pi
print('A string: "%s"' % 'Hello World')
print('An integer: %s' % 27)
print('A float: %s' % 27.0)
print('A float: %s' % pi)
print('A float: %s' % pi * 2)
print('A float: %s' % (pi * 2))
print('A float: %.2f' % pi)
print('A float: [%5.2f]' % pi)
print('A float: [%+6.2f]' % pi)
print('A float: [%+.2f]' % pi)
print('A float: [%08.2f]' % pi)
print('An integer: [%08d]' % 42)

Write similar expressions using f-strings.

Hint. See pyformat.info for examples of string formatting.

Exercise 4.1 (list aliasing and list copy)

Consider the below code. Run the code and explain the output.

a = [[1, 2], [3, 4]]
b = a
c = a[:]
b[0] = [5, 6]
c[1][1] = 7
print(a, b, c)

Hint. Try to use www.pythontutor.com.

Exercise 4.2 (infinite recursive list)

Run the below code and explain what is happing.

a = [42]
a[0] = a
print(a)

Hint. Try to use www.pythontutor.com.

Exercise 4.3 (infinite recursive indexing)

Run the below code and explain what is happing.

x = [0, 7]
x[0] = x
print(x)
print(x[1])
print(x[0][1])
print(x[0][0][1])
print(x[0][0][0][1])
print(x[0][0][0][0][1])
print(x[0][0][0][0][0][1])

Hint. Try to use www.pythontutor.com.

Exercise 4.4 (ranges and slices)

Run the below code and explain what is happing. What notations is most intuitive and consistent?

print(list(range(4, 9)))
print(list(range(9, 4, -1)))
print(list(range(8, 3, -1)))
print(list(range(4, 9)[::-1]))

Hint. Try to use www.pythontutor.com.

Exercise 4.5** (sliced ranges)

The expression range(x, y, z)[i:j:k] returns a new range(a, b, c). Note that z and k can be negative, but not zero. E.g. range(3, 18, 2)[5:2:-2] returns range(13, 7, -4).

Write a program that given integers x, y, z, i, j and k computes a, b and c. The program is not allowed to create a range explicitly, like the below.

r = range(x, y, z)[i:j:k]
a = r.start
b = r.stop
c = r.step

Start with the simple case where you assume all indexes are non-negative.

Note. To automatically test your code on random input, you can use the below code. Set -100 to 0 for the simple case.

import random

while True:
    x, y, z, i, j, k = [random.randint(-100, 100) for _ in range(6)]

    if z == 0 or k == 0:  # skip illegal input
        continue

    r = range(x, y, z)[i:j:k]

    # insert your code here

    print(f'range({x}, {y}, {z})[{i}:{j}:{k}] = {r}')

    if r != range(a, b, c):
        print('Wrong range: a b c =', a, b, c)
        break

Warning. This exercise is hard to get correct for all types of input, in particular for negative values of z and k. This exercises forces you to get a detailed understanding of what slicing a range means. Note that two ranges are considered equal if they represent the same sequence of numbers, e.g. range(2, 5, 4) == range(2, 5, 3) since they both represent a sequence only containing the number 2.

Exercise 4.6 (multiplication table)

Print a multiplication table of a given dimension. Below is shown the multiplication table for dimension 7. The program should ask the user to input the dimension of the table (≤ 100), and then print a multiplication table where all entries in a column are right aligned.

  * |  0  1  2  3  4  5  6  7
-----------------------------
  0 |  0  0  0  0  0  0  0  0
  1 |  0  1  2  3  4  5  6  7
  2 |  0  2  4  6  8 10 12 14
  3 |  0  3  6  9 12 15 18 21
  4 |  0  4  8 12 16 20 24 28
  5 |  0  5 10 15 20 25 30 35
  6 |  0  6 12 18 24 30 36 42
  7 |  0  7 14 21 28 35 42 49

Note. This is an exercise in for-loops and string formatting, see pyformat.info.

(Optional) If you are familiar with LaTeX, output LaTeX source code for a multiplication table of a given dimension that can be translated using e.g. Overleaf into a PDF figure like the below. Example output for dimension five multiplication.tex.

Exercise 4.7 (list subsequence)

Make a program that given two lists L1 and L2, determines if L1 is a subsequence of L2, i.e., if L1 can be obtained by deleting zero or more values from L2.

E.g. for L1 = [7, 2, 3] and L2 = [3, 7, 2, 5, 1, 3, 4] your program should print that L1 is a subsequence of L2 (since L1 can be obtained from L2 by deleting the first 3 together with 5, 1 and 4). For L1 = [7, 4, 3] and the same L2, your program should print that L1 is not a subsequence of L2.

Hint. First find the first occurence of L1[0] in L2, and then repeat appropriately.

Exercise 4.8 (interval union)

Make a program that given a list L of intervals with possible overlaps, where an interval is represented by a list [left endpoint, right endpoint ], computes a new list L_ of disjoint intervals but with identical union.

E.g. for L = [[1, 3], [6, 10], [2, 5], [8, 13]] the program should compute L_ = [[1, 5], [6, 13]]. It is fine to let L be a constant in the program.

Hint. Start by sorting the intervals using the builtin function sorted, and then process the intervals with respect to increasing left endpoint.

Exercise 4.9* (valid ORCID)

ORICD (Open Researcher and Contributor ID) assigns to researches a unique identifier, e.g., the ORCID of Stephen Hawkings is 0000-0002-9079-593X. An identifier consists of four blocks of digits, except for the last character in the last block that can also be X representing the value 10. The blocks are separated by the character -. The last digit in an ORCID is a checksum value, and a valid ORCID x₀x₁x₂x₃-x₄x₅x₆x₇-x₈x₉x₁₀x₁₁-x₁₂x₁₃x₁₄x₁₅ must satisfy:

(x₀ * 2¹⁵ + x₁ * 2¹⁴ + ··· + x₁₄ * 2¹ + x₁₅ * 2⁰) mod 11 = 1

Write a program that asks for an ORCID, and checks if it is a valid ORCID, i.e. checks if the length, format, and checksum are correct.

Hint. You can use the string method isdigit() to test if a string is a digit, e.g. '7'.isdigit() returns True, and in the above "mod" denotes the modulo operation that returns the remainder by division, that in Python can be computed using the % operator, e.g. 8 % 5 == 3.

Exercise 5.1 (polynomial evaluation)

A polynomial poly(x) = c_k·x^k + c_k-1·x ^k-1 + ··· + c₁·x¹ + c₀·x⁰ can be represented by a tuple (c₀, c₁, ..., c_k), e.g. the polynomial 3·x³ - 2·x² + 0·x + 5 can be represented by a tuple (5, 0, -2, 3).

Use list comprehension, enumerate and sum to evaluate a polynomial given by its coefficients. E.g. for x = 7 and coefficients (5, 0, -2, 3) your code should compute the value 936.

Exercise 5.2 (zipping names)

Given a list of first names first = ['Donald', 'Mickey', 'Scrooge'] and last names last = ['Duck', 'Mouse', 'McDuck'], use list comprehension, zip and sorted to generate an alphabetically sorted list of names 'lastname, firstname', i.e. generates the list ['Duck, Donald', 'McDuck, Scrooge', 'Mouse, Mickey'].

Exercise 5.3 (zip)

Implement your own version my_zip of zip, such that my_zip([L1, L2,..., Lk]) == list(zip(L1, L2, ...., Lk)).

Exercise 5.4 (flatten)

Make a method flatten(L) that given a list of lists L = [L1,L2,...,Lk] returns one list that is the concatenation of all lists, i.e. L1 + L2 + ··· + Lk. Your implementation should use list comprehension.

Exercise 6.1 (histogram)

Write a method histogram that given a list of values, returns a list of pairs (value, frequency).

Example. histogram(['A', 'B', 'A', 'A', 'C', 'E', 'C']) should return [('A', 3), ('B', 1), ('C', 2), ('E', 1)].

Hint. Use a dictionary and the dictionary method get.

Note. In the standard library module collections the Counter method implements the same functionality.

import collections
histogram = list(collections.Counter(['A', 'B', 'A', 'A', 'C', 'E', 'C']).items())

Exercise 6.2 (frequent long words)

This exercise extends Exercise 6.1.

Write a program that prints the most frequent words containing at least six characters occurring in a text file. E.g. for the saxo.txt file it should print something like the below.

Rank Freq. Word
====================
   1   372 should
   2   221 himself
   3   199 father
   4   196 battle
   5   187 though
   6   181 thought
   7   172 against
   8   142 before
   9   134 daughter
  10   124 country

You can use the following code to split the content of a file into a list of lower case words, ignoring everything that is not a letter in the text.

import re
txt = open('saxo.txt', encoding='utf8').read()
txt = txt.lower()
words = re.split('[^a-z]+', txt)

Hint. Use the sorted function to sort a list of tuples of the form (frequency, word), and try to use list comprehension to create such a list from a frequency dictionary.

Exercise 7.1 (average)

1. Write a function average_two(x, y) that computes the average of x and y, i.e. (x + y )/2.

2. Write a function list_average(L) that computes the average of the numbers in the list L.

3. Write a function average(x1, ..., xk) that takes an arbitrary number of arguments (but at least one) and computes the average of x1, ..., xk.

   Hint. Use a * to indicate an arbitrary argument list.

Exercise 7.2 (sum of squares)

1. Make a function that can take any number of arguments, and returns the sum of the squares of the values, i.e. square_sum(x1, x2, x3) returns x1 ** 2 + x2 ** 2 + x3 ** 2.

   > square_sum()
   0
   > square_sum(3, 4, 5)
   50
   > square_sum(1, 2, 3, 4, 5, 6, 7, 8, 9, 10)
   385
   

2. Given a list L, e.g. L = [1, 2, 3, 4], use your square_sum function to compute the sum of squares of the values in L.

Hint. Use a * to indicate an arbitrary argument list.

Exercise 7.3 (argmin)

Create a function argmin(L) that returns the index of the minimum element in a list L. If the minimum occurs multiple times in L the index of the first occurrence should be returned. If L is empty, None should be returned. E.g., argmin([3, 7, 5, 4, 2, 9, 10, 2, 8]) should return 4, since 2 is the minimum in the list and its first occurrence is at index 4.

Note: The module numpy has a function numpy.argmin providing this functionality for non-empty lists.

Exercise 7.4** (compensated summation) [optional]

The Python builtin function sum can compute the sum of a list of floats. In Python 3.12 the numerical accuracy of sum for summing floats was improved by adopting Neumaier summation - see What’s New In Python 3.12 and Raimund Hettinger's posting #100425.

    > 1/3 + 1.0 - 1.0 - 1/3  # no compensation
    -5.551115123125783e-17
    > sum([1/3, 1.0, -1.0, -1/3])  # with compensation in Python 3.12
    0.0

In this exercise you should try to reproduce this improvement.

1. Create a function my_sum(L) that takes a list of floats and returns the sum (without compensated summation), e.g.,

   > my_sum([1/3, 1.0, -1.0, -1/3])
   -5.551115123125783e-17
   

2. Extend your function with compensated summation, e.g. using Neumaier summation, so that:

   > my_sum_compensated([1/3, 1.0, -1.0, -1/3])
   0.0
   

3. Compare the output of your function against the builtin sum function for lists of random floats, say 100 floats in the range [-0.5, 0.5].

Exercise 8.1 (upper and lower cases)

Make a recursive function cases(s) that given a string s, generates a list of all possible upper and lower case combinations of the letters in the string. E.g. cases('abcB') should return a list containing the following 16 strings ['abCb', 'abCB', 'abcb', 'abcB', 'aBCb', 'aBCB', 'aBcb', 'aBcB', 'AbCb', 'AbCB', 'Abcb', 'AbcB', 'ABCb', 'ABCB', 'ABcb', 'ABcB'], not necessarily in this order.

Hint. Use .lower() and .upper() to convert a string containing one letter to lower and upper case.

Exercise 8.2 (list subsets)

Make a recursive function subsets(L) that given a list L returns a list of all subsets of L (each subset being a list). E.g. subsets([1, 2]) should return [[], [1], [2], [1, 2]]. The order of the returned lists can be arbitrary.

Exercise 8.3 (binary strings)

Create a recursive function binary(n, k) that returns a list of all binary strings of length n and containing k ones (0 ≤ k ≤ n).

E.g. binary(5, 3) should return the list ['00111', '01011', '01101', '01110', '10011', '10101', '10110', '11001', '11010', '11100'] (in any order).

Exercise 8.4 (tree relabeling)

Make a recursive function relabel(tree, new_names) that takes a tree tree and a dictionary new_names = {old_name: new_name, ...}, and returns a new tree where labels in the dictionary new_names are replaced by the corresponding values in the dictionary. Leaves not in the dictionary remain unchanged.

Example. relabel(('a', ('b', 'c')), {'a': 'x', 'c': 'y'}) should return ('x', ('b', 'y')).

Hint. Start making relabel for binary trees only. Use the method isinstance to check if a value is of class tuple or a str.

Exercise 8.5* (validate leaf-labeled binary trees)

Assume we want to represent binary trees, where each leaf has a string as a label, by nested tuples. We require the leaves are labeled with distinct non-empty strings and all non-leaf nodes have exactly two children. E.g. ((('A', 'B'), 'C'), ('D', ('F', 'E'))) is a valid binary tree.

1. Write a function validate_string_tuple(t) that checks, i.e. returns True or False, if the value t is a tuple only containing distinct strings, e.g. ('a', 'b', 'c').

2. Write a recursive function valid_binary_tree(tree) program that checks, i.e. returns True or False, if the value tree is a recursive tuple representing a binary tree as described above.

Hint. Use the method isinstance to check if a value is of class tuple or a str, and use a recursive function to traverse a tree. Collect all leaf labels in a list, and check if all leaves are distinct by converting to set.

Exercise 8.6* (subtree extraction)

Make a recursive function extract(tree, leaves) that takes a binary tree tree and a set of leaves, generates a new binary tree only containing the leaves in leaves, i.e. repeatedly all other leaves are pruned, previous internal nodes with no children are removed, and previous internal nodes with only one child are replaced by the child.

Example. extract(((('a', 'b'), 'c'), ((('d', 'e'), 'f'), 'g')), {'a', 'c', 'd', 'f', 'g'}) should return (('a', 'c'), (('d', 'f'), 'g')) (see illustration below where leaves 'b' and 'e' have been removed).

           before                   after
             /\                       /\
            /  \                     /  \
           /    \                   /    \
          /      \                 /\     \
         /        \               /  \     \
        /          \            'a'  'c'   /\
       /            \                     /  \
      /\            /\                   /    \
     /  \          /  \                 /\    'g'
    /    \        /    \               /  \
   /\    'c'     /\     \            'd'  'f'
  /  \          /  \    'g'
'a'  'b'       /    \
              /\    'f'
             /  \
           'd'  'e'

Exercise 9.1 (bitonic minimum)

We call a list L = [x1, ..., xn] bitonic, if there exists a k, 1 < k < n, such that

x1 > x2 > ··· > x{k-1} > xk < x{k+1} < ··· < xn,

i.e. xk is the minimum of the list. Write a method bitonic_min that given a bitonic list, returns the minimum of the list. Your implementation should use binary search (i.e. you cannot use the Python builtin min function).

Example. bitonic_min([10, 7, 4, 2, 3, 5, 9, 11, 13, 15]) should return 2.

Exercise 9.2 (print tree)

Assume we represent a tree by a recursive tuple, consisting of the name of the root followed by one recursive tuple for each of the children. Note that all nodes have a label (not only the leaves), and that a node with k children is represented by a tuple of length k + 1. Write a program that prints the tree with one label per line and with appropriate indentation, like below.

Example. ('root', ('node 1',), ('node 2', ('node 2.1',), ('node 2.2',)), ('node 3',)) should be printed as

--root
  |--node 1
  |--node 2
  |  |--node 2.1
  |  |--node 2.2
  |--node 3

Hint. Write a recursive method and pass a string as an argument with the prefix to be printed in front of all lines generated by the recursive call.

Exercise 9.3 (maze path)

In this exercise you should code a recursive maze solver, that does a recursive search for the path from 'A' to 'B' in a rectangular maze. The program should read from input a maze represented by first a single line containing two numbers, the number of rows n and columns m of the maze, followed by n rows each containing a string of length m representing the maze, where '#' is a blocked cell, 'A' denotes the start cell, 'B' the end cell, and '.' a free cell ('A' and 'B' are also free cells). Given a free cell one can move to an adjacent free cell horizontally and vertically but not diagonally.

An example input:

11 19
#######A###########
#.......#.#...#...#
#.###.###...#.#.#.#
#...#.....#.#...#.#
#.#.###.#.#.#.###.#
#.#.....#...#.#...#
#.###########.#.#.#
#.#.#.....#...#.#.#
#.#.#####.#####.#.#
#.........#.....#.#
###############B###

The program should output the string 'no path' if there exist no path from 'A' to 'B' in the maze. If there exists a path, a solution should be printed with 'x' marking the path from 'A' to 'B'. A possible solution to the above maze is:

#######A###########
#....xxx#.#xxx#xxx#
#.###x###xxx#x#x#x#
#...#xxxxx#.#xxx#x#
#.#.###.#.#.#.###x#
#.#.....#...#.#xxx#
#.###########.#x#.#
#.#.#.....#...#x#.#
#.#.#####.#####x#.#
#.........#....x#.#
###############B###

Note. In the lecture the solution only identified if there was a path from 'A' to 'B'.

Hint. One solution is to modify the solution from the lecture, and only make recursive calls when a solution has not been found yet, and to update the maze before returning from a recursive call. Use print('\n'.join(maze)) to print the maze.

Exercise 9.4** (deepcopy)

In this exercise you should implement your own version of the deepcopy operation from the module copy for lists. Recall that when copying a list L using L.copy(), only a copy of the list will be created. The new list will point to the same elements as L, which might cause unexpected behavior when these are mutable structures, like recursive lists. The operation copy.deepcopy also makes a recursive copy of such recursive lists.

The difference is illustrated by the following code:

import copy
L1 = [[1], [2]]
L2 = L1.copy()
L3 = copy.deepcopy(L1)
L1[0][0] = 3
print(f'{L1=} {L2=} {L3=}')

that prints

L1=[[3], [2]] L2=[[3], [2]] L3=[[1], [2]]

Your task is to implement your own function deepcopy that creates such a recursive deep copy of recursive lists.

Hint. Recall that the same list can be referred to multiple times, and that there can be cyclic references among the lists, like in the following example.

L = [[1], [2], [3]]
L[2] = L

To handle the copying of such recursive structures it is important to know that each list L has a unique id id(L). E.g.

print(f'{L=} {id(L)=} {id(L[0])=} {id(L[1])=} {id(L[2])=}')

could print

L=[[1], [2], [...]] id(L)=2373651524288 id(L[0])=2373623114048 id(L[1])=2373623104832 id(L[2])=2373651524288

Note that L and L[2] have identical ids, since they refer to the same list.

Example.

L1 = [[1], [2], [3]]
L2 = deepcopy(L1)
L1[1] = L1[0]
L1[2][0] = L1
L3 = deepcopy(L1)
L3[0][0] = 7
print(f'{L1 = } {L2 = } {L3 = }')

should print

L1 = [[1], [1], [[...]]] L2 = [[1], [2], [3]] L3 = [[7], [7], [[...]]]

Exercise 10.1 (my_map)

In this exercise the goal is make your own implementation of Python's builtin map function.

1. Make a function my_map that takes two arguments, a function f and a list [x1, ..., xn], and returns the list [f(x1), ..., f(xn)].

   Example. my_map(lambda x: x ** 3, [3, 2, 4])) should return [27, 8, 64].

2. Make a function my_map_k that as arguments takes a function f requiring k ≥ 1 arguments and k lists L1, ..., Lk, and returns the list [f(L1[0], ..., Lk[0]), ..., f(L1[n-1], ..., Lk[n-1])], where n is the length of the shortest Li list.

   Hint. Use Python's * notation to handle an arbitrary number of lists as arguments.

   Example. my_map_k(lambda x, y, z: x * y * z, [3, 2, 5], [2, 7, 9], [1, 2]) should return [6, 28].

Note. Your solution should not use the builtin map function.

Exercise 10.2 (string sorting)

Write a function str_sort that sorts a list of strings, such that the strings are sorted with respect to the number of distinct letters ('a' - 'z') there are in the strings. Strings with an equal number of distinct letters after converting to lower case should apper in alphabetical order.

Example.

str_sort(['AHA', 'Oasis', 'ABBA', 'Beatles', 'AC/DC', 'B. B. King', 'Bangles', 'Alan Parsons'])

should return

['ABBA', 'AHA', 'AC/DC', 'Oasis', 'B. B. King', 'Beatles', 'Alan Parsons', 'Bangles']`.

Hint. Use len(set(X)) to find the number of different elements in a list X.

Exercise 10.3 (binary search)

Assume you have a function f mapping integers to True and False, and there exists an integer x such that f(y) == False for y < x, and f(y) == True for y ≥ x. Write a function binary_search(f, low, high) that returns the smallest x where f(x) == True, provided f(low) == False and f(high) == True. The function should use binary search, like in Exercise 9.1 (bitonic minimum).

Example. binary_search(lambda x: x * x >= 1000, 0, 1000) == 32 == ceil(sqrt(1000)).

Assume now f is a function from floats to floats that is strictly decreasing in an interval [low, x_min] and strictly increasing in the interval [x_min, high] for some real number x_min and integers low and high. Use your function binary_search to write a function local_min(f, low, high) that returns the smallest integer x in the range ]low, high] such that f(x) < f(x + 1), i.e. a local minimum of f.

Example. local_min(lambda x: (x - 3.5) ** 2 - 7 * x, -1000, 1000) returns 7.

Exercise 10.4* (foldr)

In this exercise the goal is to make an implementation of foldr (fold right). Python's reduce function is often called foldl (fold left) in other programming languages, that given a function f and a list [x1, x2, x3, ..., xn] computes f(f(···f(f(x1, x2), x3)···), xn).

The function foldr should instead compute f(x1, f(x2, f(x3, f(···f(xn-1, xn)···)))).

The difference between folding left and right is illustrated by applying the power function to the list [2, 2, 2, 2], where ((2 ** 2) ** 2) ** 2 == 256 whereas 2 ** (2 ** (2 ** 2)) == 65536.

import functools
foldl = functools.reduce

def foldr(f, L):
    # your code

print(foldl(lambda x, y: x ** y, [2, 2, 2, 2]))     # prints 256
print(foldr(lambda x, y: x ** y, [2, 2, 2, 2]))     # should print 65536
print(foldr(lambda x, y: x ** y, [2, 2, 2, 2, 2]))  # value with 19729 digits

The foldr function does not appear in the Python standard library but is standard in other programming languages, in particular functional programming languages like Haskell and ML.

Note. You can implement foldr both with a loop and recursively.

Exercise 11.1 (PersonReader)

Implement a class PersonReader supporting the following methods:

• input() asks the user for the name and year of birth of a person at shell prompt (using the builtin input function).

• __str__ that returns the string 'name (year)' (e.g. to be used by the print method when applied to a PersonReader).

Example.

> M = PersonReader()
> M.input()
Name: Margrethe
Born: 1940
> print(M)
Margrethe (1940)

Exercise 11.2 (Stopwatch)

Implement a class Stopwatch that creates a timer that can measure the total between calls to the methods start and stop. The methods that should be supported are:

• start() start the stopwatch.

• stop() stop the stopwatch.

• lap() record the current time as a lap time.

• total_time() return the time between last start and subsequent call to stop. If the stopwatch is still running, return time since last call to start and the current time.

• lap_times() return a list of the lap times. If there have been k calls to lap between the calls to start and stop, it should return a list of the k+1 lap times. The sum of the lap_times should equal the time of total_time.

It can be assumed that start is the first method that will be called.

Hint. Use the method time in module time, i.e. add from time import time to your code. The function time() returns the number of seconds since, typically, January 1, 1970, 00:00:00.

Exercise 11.3 (2D vector)

In this exercise you should implement a class Vector for storing 2D vectors with the two vector coordinates as the attributes x and y. The class should have the following methods:

• A constructor __init__ where it is possible to create a new vector using Vector(x, y).

• length() returning the length of the vector, i.e. sqrt(x ** 2 + y ** 2). Hint. from math import sqrt.

• add(other_vector) return a new vector that is the result of adding two vectors.

• Redefine + so that vector1 + vector2 returns a new vector that is the sum of the two vectors (i.e. define __add__).

• mult(factor), where factor is an int or float, should return a new vector Vector(x * factor, y * factor).

• dot(vector) should return the dot product with another vector, i.e. x * vector.x + y * vector.y.

• Define the * operator so that vector * number returns vector.mult(number) whereas vector1 * vector2 returns the dot product of the two vectors (i.e. define __mul__).

• Define __rmul__ so that it possible to write number * vector. The result should be the same as vector * number.

• Define __str__ to return the string '<x, y>' where x and y are the coordinates of the vector.

Exercise 12.1 (geometric shapes)

Make a class Shape that represent an abstract geometric shape. Concrete shapes, like circles, axis-aligned rectangles, and triangles should be defined as subclasses of Shape. The class Shape should only define a method fatness that depends on methods area and perimeter that should be defined in subclasses:

• fatness() return 4·π·area / perimeter².

Subclasses should implement the following methods (but note the method fatness):

• __init__ initialize the geometric object. The arguments to __init__ will depend on the geometric shape.

• __str__ return a string describing the object, e.g. Circle(radius=3, center_x=4, center_y=5).

• area() return the area of a geometric object.

• perimeter() return the length of the perimeter of the geometric object.

• contains(x, y) returns if the point (x, y) is contained within the shape.

Create classes Circle, Rectangle, and Triangle, each inheriting from class Shape. Implementing class Triangle is optional (the methods area and contains require some amount of math, with solutions easily to find on the internet). For each subclass implement the methods __int__, __str__, area, perimeter, and contains.

It should be possible to create instances of the geometric objects (calling __init__) as follows:

• Circle(radius, center_x, center_y)

• Rectangle(min_x, max_x, min_y, max_y)

• Triangle(x0, y0, x1, y1, x2, y2)

Example.

> shapes = [Rectangle(0, 10, 0, 1), Circle(4, 1, 4), Triangle(1, 2, 1, 4, 2, 3)]
> [str(s) for s in shapes]
['Rectangle((0, 0), (10, 1))', 'Circle(radius=4, center_x=1, center_y=4)', 'Triangle((1, 2), (1, 4), (2, 3))']
> [s.area() for s in shapes]
[10, 50.26548245743669, 1.0]
> [s.perimeter() for s in shapes]
[22, 25.132741228718345, 4.82842712474619]
> [s.fatness() for s in shapes]
[0.25963575649502424, 1.0, 0.5390120844526473]
> [s.contains(1,1) for s in shapes]
[True, True, False]

Exercise 13.1 (sum of two integers)

Write a program that as input takes a single line with two integers and outputs their sum. A valid input line consist of two integers separated by one or more white spaces. Input can be preceded and followed by white spaces. The program should repeat asking for input until a valid input is given.

Input two integers, separated by space: 2 a
invalid input
Input two integers, separated by space: 2 3.0
invalid input
Input two integers, separated by space: 2 3
Sum = 5

Hint. Use exceptions to handle illegal input.

Exercise 13.2 (transposing)

In this exercise we assume that a file stores a matrix, where the rows are stored in consecutive lines in the file, and where column values are separated by ;. Your task is to make a program that writes the transposed matrix to another file - see example below.

Input:

1;2;3;4
5;6;7;8
9;10;11;12

Output:

1;5;9
2;6;10
3;7;11
4;8;12

The program should ask the user for the name of an input file and the name of an output file, read the matrix in the input file, and write the transposed matrix to the output file.

Your solution should handle the following potential errors.

• If input file does not exist, report this to the user and start over.

• If output file already exists, warn the user, and ask the user to confirm to overwrite the existing file.

• If the lines in the input file have a different number of values, i.e. the input is not a valid matrix, report this to the user, and start over without writing any output.

Hint. Use the string method split to split a line into a list of values.

Exercise 13.3 (grade statistics)

In this exercise you should write a program that reads two files: one respectively containing the names and address of students, and one containing exam results. The output of the program should be a summary of the exam performances.

The student list is stored in a file, with one student per line, consisting of the three fields, separated by ; : the unique student id, name and address.

107;Donald Duck;Duck Steet 13, Duckburg
243;Mickey Mouse;Mouse Street 42, Duckburg
465;Goofy;Clumsy Road 7, Duckburg
777;Scrooge McDuck;Money Street 1, Duckburg

The second file contains the list of exam results, consisting of a line per grade given, consisting of a triple, with values separated by ; : student id, course name, and grade.

107;Programming;10
107;Mathematics;8
107;Computability;7
243;Programming;10
243;Computer forensic;10
243;Computability;9
465;Mathematics;6

The program should print a summary like the below:

Student id Name            Average #Courses
===========================================
107        Donald Duck        8.33        3
243        Mickey Mouse       9.67        3
465        Goofy              6.00        1
777        Scrooge McDuck     0.00        0

Exercise 13.4 (unicode lookup)

There exist many special Unicode characters, that can be used in Python. E.g., the following prints a snowman symbol (☃).

print('\N{snowman}')

or

import unicodedata
print(unicodedata.lookup('snowman'))

In this exercise you should write a program that finds all Unicode names, containing a substring. Your task is to download the file https://www.unicode.org/Public/15.0.0/ucd/UnicodeData.txt, that e.g. for the snowman symbol contains the line:

2603;SNOWMAN;So;0;ON;;;;;N;;;;;

The first value is a hexadecimal (base 16) value representing the unicode number. To print a snowman, you can use print(chr(int('2603', 16))).

Your program should ask for a substring, and print all symbol names and the symbol that contain the substring, e.g.,

Unicode search: snowman
SNOWMAN ☃
SNOWMAN WITHOUT SNOW ⛄
BLACK SNOWMAN ⛇

Exercise 13.5* (subset sum)

In this exercise we consider the subset sum problem. Write a function subset_sum(x, L) that as input takes a value x and a list of values L. The function should return a list L_ with a subset L where sum(L_) == x if such a set L_ exists, otherwise None should be returned.

Example.

> print(subset_sum(12, [2, 3, 8, 11, -1]))
[2, 11, -1]
> print(subset_sum(6, [2, 3, 8, 11, -1]))
None

The subset sum is known to be a computationally hard problem that essentially only can be solved by considering all 2^|L| possible subsets of the input list L.

Hint. Write a recursive function that generates all possible subsets, and raise an exception (ideally user defined) during the recursion when the first solution has been found. Do not generate an explicit list of all subsets, since this will quickly lead to MemoryError exceptions.

Exercise 14.1 (identical pairs)

Write a method identical_pairs(L) that given a list L returns the number of index pairs (i, j) where i < j and L[i] == L[j]. E.g., identical_pairs([3, 2, 3, 1, 2, 3, 1]) should return 5.

Your code should be able to handle inputs with a million values.

Write tests for your code.

Hint: Apply sorted to the list and only do one scan over the list to compute the result.

Exercise 15.1 (integer rounding)

Create a function decorator @integer_round that can be applied to a function returning a float. The decorated function should apply the builtin function round to the returned float value.

An example using the decorator is

@integer_round
def f(x):
    return x ** 0.5  # square root

where f(30) should return 5, and f(31) should return 6.

Exercise 15.2 (decorator returns int)

Create a function decorator @enforce_integer_return that checks if a function returns a value of type int and raises an AssertionError if the result is of a different type. The decorator could e.g. be used as in the example below.

> @enforce_integer_return
  def my_sum(x, y):
      return x + y

> my_sum(19, 23)
42

> my_sum(1, 2.5)
...
AssertionError: result must be int

Exercise 15.3 (box it)

Create a decorator @BoxIt for functions returning a string. The output of a function returning a string should be converted into a new string, with the output put into a 'box' (see example below). You can assume that the string returned by a function only consist of a single line of text, i.e. the string does not contain '\n'.

@BoxIt
def plus(x, y):
    return f'The sum of {x} and {y} is {x + y}'

print(plus(3,4))

should print the following

---------------------------
| The sum of 3 and 4 is 7 |
---------------------------

Exercise 15.4 (multiline box it) [optional]

Generalize your solution to Exercise 15.3, so that it can handle multiline output.

@BoxIt
def test():
    return 'This\n   is a\n      test'

@BoxIt
@BoxIt
def plus(x, y):
    return f'{x} + {y} = {x + y}'

print(test())
print(plus(3, 4))

should print the following

+------------+
| This       |
|    is a    |
|       test |
+------------+
+---------------+
| +-----------+ |
| | 3 + 4 = 7 | |
| +-----------+ |
+---------------+

Exercise 15.5** (decorator composition) [optional]

If you repeatedly apply the same set of decorators to your functions, it might be convenient to compose these decorators into one decorator.

Recall that:

@dec3
@dec2
@dec1
def my_func(*args):
    ...

is equivalent to

def my_func(*args):
    ...

my_func = dec3(dec2(dec1(my_func)))

One could compose the three decorators into one decorator dec_composed as

def dec_composed(f):
    return dec3(dec2(dec1(f)))

and using this new decorator as

@dec_composed
def my_func(*args):
    ...

In this exercise you should make a function compose that takes a sequence of decorator functions, and composes them into one new decorator. The above decorator composition could then have been written as:

dec_composed = compose(dec3, dec2, dec1)

Alternatively one could use compose as a decorator with arguments

@compose(dec3, dec2, dec1)
def my_func(*args):
    ...

The below example uses the compose function in the two different ways.

def double(f):
    def wrapper(*args):
        return 2 * f(*args)

    return wrapper

def add_three(f):
    def wrapper(*args):
        return 3 + f(*args)

    return wrapper

@compose(double, double, add_three)
def seven():
    return 7

print(seven())  # prints 40

my_decorator = compose(double, double, add_three)

@my_decorator
def seven():
    return 7

print(seven())  # prints 40

Note. The function compose mathematically corresponds to function composition.

Exercise 16.1 (coins)

In this exercise we would like to obtain some currency amount using the fewest coins available in the currency. We assume that the set of different coin values of the currency is represented by a tuple, e.g. coins = (1, 2, 5, 10, 20) could represent the Danish coins.

In this exercise you can assume that all amounts and coins have integer values, and that there is coin of value 1 in the currency - this guarantees that all values can be expressed using the available coin values. Furthermore you might assume that all amounts are ≤ 200.

Consider the above coins. The amount 33 can be achieved in many different ways, e.g. 10 + 10 + 5 + 5 + 1 + 1 + 1 and 20 + 10 + 2 + 1. The last sum is a solution using the fewest coins.

A simple greedy strategy to construct a list of coins for a given value, is to repeatedly take the coin with largest value until the remaining value is less that the value of the largest coin. Then repeatedly take the second largest valued coin as long as possible, etc. For some set of coins this strategy is guaranteed to always find an optimal solution, like for the above tuple coins. But in general this strategy will not always find the optimal strategy, e.g. for the value 14 and possible coins (1, 7, 10), the greedy strategy will find the solution 10 + 1 + 1 + 1 + 1, whereas an optimal solution using the fewest coins is 7 + 7.

1. Implement a function change_greedy(value, coins) that implements the greedy change strategy, and returns a list of integers, each integer in coins, and with sum equal to value.

   Example. change_greedy(35, (1, 7, 10)) should return [10, 10, 10, 1, 1, 1, 1, 1].

2. Implement a recursive function number_of_coins(value, coins) that returns the number of coins in an optimal solution. The function can implement the following recursive expression:

   • If value = 0: number_of_coins(value, coins) = 0
   • If value > 0: number_of_coins(value, coins) = 1 + min_{coin in coins where coin ≤ value} number_of_coins(value - coin, coins)

   To speed up your computation use memoization, e.g. using the decorator @memoized (without memoization, the second example below will run for a very very long time).

   Example. number_of_coins(35, (1, 7, 10)) should return 5, and number_of_coins(100, (1, 2)) should return 50.

3. Implement a recursive function change(value, coins) that returns an optimal solution, i.e. a list of integers, each integer in coins and where the sum equals value. One approach could be to modify your function number_of_coins appropriately to return a list of coins instead of a number.

   Example. change(35, (1, 7, 10)) could return the list [1, 7, 7, 10, 10].

The depth of the recursion when running the above recursive functions depends on the parameter value, and it is very likely you will get a RecursionError: maximum recursion depth exceeded when trying to compute number_of_coins(1000, (1,)). In the final question you should convert your change function into an iterative solution that systematically fills out the 'memoization table'.

4. Implement a function change_iterative(value, coins) that returns an optimal solution. The function should fill out a table of solutions for increasing values of value.

   Example. change_iterative(12345, [1, 2, 5, 10, 20]) could return [20, 20, ..., 20, 20, 5].

Exercise 16.2 (missing spaces) [optional]

Assume you have a text text where all spaces have been lost. To recover the spaces you have a dictionary words (a Python set) containing known words. The original text can also contain words not in the dictionary. The goal is to try to recover the spaces as good as possible: Find in the string non-overlapping occurrences of words from the dictionary, such that the total number of words identified plus the number of characters in the text not contained in any of the identified word occurrences is minimized. Equivalently if we put '_' between each word and character not in a word occurrence, then we would like to return a shortest such string, i.e. minimize the number of '_' in the output.

text = 'aduckcrossestheroad'
words = {'a', 'ad', 'cross', 'duck', 'est', 'he', 'road', 'the'}
solution_optimal = 'a_duck_cross_est_he_road'
solution_greedy = 'ad_u_c_k_cross_est_he_road'

1. Implement a greedy strategy reading the text from left to right, always trying to find the longest possible word in the dictionary starting at the current position.

2. Implement a dynamic programming solution, that finds an optimal solution. One systematic (non-recursive) approach is to create an array solutions, where you for increasing index i, from 0 to len(text), compute an optimal solution for text[:i] and store this in solutions[i].

Note. As a dictionary of Danish words, you can try to download the list of Danish words from the webpage of Dansk Sprognævn. Save the word list as words.txt, and run the below code to get the word list into your program as a set of words (in lower case without prefixes '1. ', '2. ', etc. and with spaces and periods removed).

import re
with open('words.txt', encoding='utf-8') as f:
     words = f.readlines()
words = [w.split(';')[0] for w in words]
words = {re.sub('^[1-9][.] |[ .]', '', w).lower() for w in words}

To get a sample text without spaces, your can e.g. use the following code.

text = '''Danish multi line text sample, e.g. from https://da.wikipedia.org/wiki/Aarhus'''
text = re.sub('[ \n,.]', '', text).lower()

Exercise 17.1 (Jupyter install)

Install and lunch Jupyter.

Exercise 17.2 (getting started with Jupyter)

Create a simple Python 3 document in Jupyter. Create a Markdown cell with some text, possibly using various formatting (see also the Help menu in the Jupyter window for syntax). Create a cell with some simple Python 3 code. Learn the difference between Shift-Enter, Ctrl-Enter and Alt-Enter (see topic Keyboards Shortcuts in the Jupyter Help menu).

Exercise 17.3 (Jupyter plotting)

Plot the function f(x) = 100·(x - 3)² + e^x for the x in ther range [0, 10] using matplotlib.pyplot in Jupyter.

Exercise 17.4 (Jupyter function minimization)

Find the minimum of the function in Exercise 17.3 using scipy.optimize.minimize. Extend the plot in Exercise 17.3 to illustrate the minimum, e.g. using a dot.

Exercise 18.1 (numpy)

1. Generate two 5x5 matrices with entries drawn from a standard normal distribution (mean 0, variance 1). numpy.random.normal might come in handy here. Find the inverse of the matrices. Check by matrix multiplication, that it is in fact the inverses you have found.

2. Find the mean of each row and each column of the matrices without using loops. numpy.mean might come in handy here.

3. Create a 100x100 matrix with entries drawn from the uniform distribution between 0 and 1. Find all rows where the sum exceeds 55. Find both the row index and the sum. (Try to have a look at the functions numpy.sum and numpy.where).

Exercise 18.2 (computing pi using sampling)

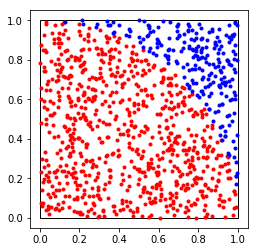
In this exercise we want compute an approximation of π using random sampling: Given a uniformly selected random point in the unit-square [0,1]², it has probability π / 4 to have distance ≤ 1.0 to (0,0), i.e. to be within the circle with radius one and center located in the origo.

1. Compute an approximation of π from sufficiently many uniform samples from the unit-square [0,1]². You solution must use numpy. You can e.g. generate a 2 x 1000000 matrix with random values and use some of the functions numpy.random.random,numpy.random.uniform, numpy.linalg.norm, numpy.average, numpy.sum, numpy.size, ...

2. Use numpy and matplotlib to plot a figure of your sample, like in the figure. Try to use numpy masking (Boolean array indexing) to select the different colors.

Exercise 18.3 (polynomial fit)

Consider the below list L of 2D points. Apply numpy.polyfit for different degrees of the polynomial fitting, and find the minimum degree polynomial where the maximal vertical distance between a point (x, y) in L and the polynomial poly is at most 1, i.e. abs(y - poly(x)) <= 1 for all (x, y) in L. Plot the data points and the different polynomial approximations. Present your work in Jupyter.

L = [(2, 3), (5, 7), (4, 10), (10, 15), (2.5, 5), (8, 4), (9, 10), (6, 6)]

Exercise 19.1 (linear program)

Solve the below linear program using scipy.optimize.linprog.

Maximize (objective function)

350·x₁ + 300·x₂

subject to

x₁ + x₂ ≤ 200
9·x₁ + 6·x₂ ≤ 1566
12·x₁ + 16·x₂ ≤ 2880
x₁ ≥ 3
x₂ ≥ 7

Hint. The maximum of the objective function is 66100.

Exercise 20.1 (huge ranges)

Explain the difference between sum(range(1_000_000_000)) and sum(list(range(1_000_000_000))).

Exercise 20.2 (subsequence)

Create a function is_subsequence(X, Y) that takes two iterable sequences, and returns if X is a subsequence of Y, i.e., if X can be obtained by deleting zero or more characters from Y. Your solution should only assume that the sequences are iterable, i.e., you can call iter on them but you cannot index into the sequences.

> is_subsequence([1,3,5], [1,2,4,5])
False
> is_subsequence([3,10,8,5], [2,8,3,10,5,8,5,11])
True
> from itertools import count, islice
> is_subsequence(islice(count(6, 12), 100), islice(count(0, 2), 1000))
True
> is_subsequence(islice(count(6, 13), 100), islice(count(0, 2), 1000))
False

Exercise 20.3 (Fibonacci numbers - generator and iterator)

1. Fibonacci generator: Make a generator fib(n) to generate the first n Fibonacci numbers. Your solution should use the yield keyword.

   > print(list(fib(10)))
   [1, 1, 2, 3, 5, 8, 13, 21, 34, 55]
   > print(sum(fib(100)))
   927372692193078999175
   

2. Fibonacci iterator: Create an iterable class Fibonacci with methods __init__ and __iter__ and an iterator class FibonacciIterator with methods __init__ and __next__. The object creation Fibonacci(n) should create an iterable object for the first n Fibonacci numbers, and the __iter__ method should return an instance of FibonacciIterator. In the class FibonacciIterator implement the method __next__, that either returns the next Fibonacci number or raises a StopIteration exception.

   > f = Fibonacci(5)
   > type(f)
   <class '__main__.Fibonacci'>
   > it = iter(f)
   > type(it)
   <class '__main__.FibonacciIterator'>
   > next(it)
   1
   > next(it)
   1
   > next(it)
   2
   > next(it)
   3
   > next(it)
   5
   > next(it)
   StopIteration
   > for _ in range(3):
         for x in f:
             print(x, end=' ')
   1 1 2 3 5 1 1 2 3 5 1 1 2 3 5
   

Exercise 20.4 (subsets generator)

Make a generator version of the subsets function (see Exercise 8.2) using the yield keyword.

Exercise 20.5 (subset sum generator)

Write a generator function subset_sum(x, L) that reports all subsets of L with sum x (see also Exercise 13.4). Your solution should use the generator function from Exercise 20.3.

Exercise 20.6 (permutations generator)

Make a generator function permutations(L) that given a list L generates all permutations of L. The method should use the yield keyword. The order of the returned lists can be arbitrary.

Example. permutations([1, 2]) should return [[1, 2], [2, 1]].

Note. An implementation of the permutations generator also exists in the standard library itertools (but in this exercise you should of course write the function from scratch). An example usage is:

> from itertools import permutations
> permutations([1, 2, 3])
<tertools.permutations object at 0x03C4CA80&gt;
> list(permutations([1, 2, 3]))
[(1, 2, 3), (1, 3, 2), (2, 1, 3), (2, 3, 1), (3, 1, 2), (3, 2, 1)]

Exercise 20.7* (linked list)

Lists are fundamental to Python, but a shortcoming of Python's builtin lists is that L.extend(L2) takes time proportional to the number of elements added to L from L2. In this exercise you should implement the alternative linked lists, more precisely cyclic singly linked lists.

Implement two classes Node and LinkedList.

Node objects should have two data attributes element and next. The class Node should have one method:

• n = Node(element) should create a new node with element element and next pointing to the node itself (implement __init__).

LinkedList objects should have a single data attribute last pointing to the last node on the cyclic linked list. If a list is empty, last should be None.

The class LinkedList should support the following methods (all only changing a constant number of data attributes):

• L = LinkedList() should construct an empty list (implement __init__).

• L.empty() returns if the list L is empty, i.e. contains no nodes.

• L.push(e) adds a new node at the front of the list containing e.

• L.pop() removes the first node from the front of the list and returns the element the node contained.

• L.__iter__() should be a generator to iterate over all the elements in the list.

• L.extend(L2) inserts the linked list L2 at the end of the linked list L. Sets L2.last = None.

Example. The figure shows the linked list L after executing the below first three push operations.

> L = LinkedList()
> L.push(1)
> L.push(2)
> L.push(3)
> list(L)  # constructs a Python list by iterating over the elements of L
[3, 2, 1]
> L.pop()
3
> L2 = LinkedList()
> L2.push(5)
> L2.push(6)
> L2.push(7)
> L.extend(L2)
> L2.empty()
True
> list(L2)
[]
> list(L)
[7, 6, 5, 2, 1]

Note. Linked lists are standard in many languages, e.g. in C++ as std::list and in Java java.util.LinkedList - just not in Python. (Doubly) linked lists benefit from being efficient to concatenate and to support the efficient deletion of an arbitrary element in the middle of the list, but suffer from having no efficient index lookup.

Exercise 21.1* (job scheduling)

Assume you have n jobs where each job needs to be performed on some machine at a particular interval of time, i.e. the i-th task has a start time start_i and finishing time end_i. You are going to buy a number of identical machines and to schedule the jobs on the machines such that two jobs scheduled on the same machine do not have overlapping time intervals (not even at the endpoints).

The problem is to minimize the number of machines required to execute all the n jobs.

The below list of eight time intervals for eight jobs can be scheduled on three machines as shown in the figure.

[(1, 5), (6, 7), (3, 8), (2, 4), (8, 10), (5, 9), (1, 2), (9, 10)]

Create a module job_scheduling containing the following two functions solve and visualize.

1. Write a function solve(jobs) that given a list of intervals (start_i, end_i) returns a list schedule with len(jobs) == len(schedule) and where schedule[i] is the machine to execute job i on. E.g. one possible minimal schedule for the above intervals is:

   [2, 2, 1, 3, 2, 3, 1, 1]
   

2. Write a function visualize(jobs, schedule) that visualizes the solution using matplotlib.pyplot, e.g. as in the figure.

3. How long time does it take to find a schedule of 10⁶ elements (e.g. using the below code)?

   from job_scheduling import solve
   from random import randint
   
   jobs = [(i + randint(0,100), i + randint(100,200)) for i in range(1000000)]
   
   schedule = solve(jobs)
   print(max(schedule))
   

Hint. Sort the jobs by start time and assign the jobs to machines by considering them in increasing order of start time. Use the module heapq to keep track of the currently active jobs and their finishing times. Whenever the earliest finishing time of an active job is earlier than the start time of the next job to schedule, terminate this active job and release its machine to a pool of free machines.

Exercise 22.1 (reading csv)

Extend your code for Handin 9 (maximum flow) to read the graphs from CSV files. For 19.2(a) the first line should contain the names of the source and sink nodes, whereas for 19.2(b) the first line should contain the name of the source, sink, and the flow value.

Exercise 22.2 (re.split)

In this exercise you should use the split method in the module re to split a string into a list of substrings, based on a regular expression capturing the set of separator symbols !, ?, ;, :, . and ,, where a separator string is one or more consecutive of these symbols together with zero or more white space before and after the separator. An example is the below.

'this.was a test!, and here comes   :   the rest'
['this', 'was a test', 'and here comes', 'the rest']

Hint. See the documentation for module regular expressions.

Exercise 22.3 (regular expression)

In exercise 16.2 (missing spaces) the problem statement includes the below lines. Explain what the following lines do.

words = [w.split(';')[0] for w in words]
words = {re.sub('^[1-9][.] |[ .]', '', w).lower() for w in words}

Exercise 22.4 (find frequent phrases)

Find all occurrences of the form "the word" in the file saxo.txt (see Exercise 4.8) using a regular expression (convert the string to lower case before searching). Generate a list of the most frequent occurrences, like the below:

410 the king
138 the danes
121 the enemy
110 the same
 87 the other
 83 the first
 80 the most
 64 the sword
 63 the battle
 62 the sea
 61 the man

Note. There might me a line break between the and word (e.g. the king only occurs 387 times on a single line).

Exercise 23.1 (World Bank data)

Plot the development in the population in the Scandinavian countries (Norway, Denmark, Sweden, Finland, Iceland) since 1960 until last year.

Use the pandas data reader for the World Bank data to get the population data. The indicator is SP.POP.TOTL.

Hint. Use the data frame methods unstack and plot.

Exercise 24.1 (whiten)

Create your own implementation of scipy.cluster.vq.whiten.

Assume we have n data points, each being a d-dimensional vector p_i, and let p_ij denote the j-th coordinate of the data point i. For each coordinate we compute the mean µ_j = (∑_i=1..n p_ij) / n, the variance σ_j² = (∑_i=1..n (p_ij - µ_j)²) / n, and the standard deviation σ_j = (σ_j²)^0.5. The method whiten replaces p_ij by p_ij / σ_j.

You can either implement your method with plain Python using lists of tuples representing data-points or using numpy. For numpy be aware of the keyword arguments axis and keepdims for the numpy.sum method.

> whiten([(1.9, 2.3, 1.7),
          (1.5, 2.5, 2.2),
          (0.8, 0.6, 1.7)])
[[4.179442778108569, 2.698113510169924, 7.212489168102781],
 [3.299560087980449, 2.9327320762716567, 9.333809511662423],
 [1.7597653802562396, 0.7038556983051976, 7.212489168102781]]

Exercise 24.2 (centroid for one cluster)

Prove that the centroid c of a d-dimensional point set C containing n points is the average point, i.e. the point c = (∑_p∈C p) / n minimizes the distortion ∑_p∈C |p - c|², where |p - c|² = ∑_j=1..d (p_j - c_j)².

Note. This is a plain math exercise.

Hint. Observe that it is sufficient to consider each coordinate independently and find the minimum point using differentiation.

Exercise 24.3* (k-means clustering in 1D)

Assume we have a sorted list L of N ≥ 1 real values x₁ ≤ ··· ≤ x_N, and we want to solve the k-means problem for this input optimally, i.e. to find K centroids c₁,...,c_K, 1 ≤ K ≤ N, such that the distortion ∑_i=1..N min_j=1..K (x_i - c_j)² is minimized.

Let D(k, n) denote the minimum distortion for k centroids for x₁, ...,x_n, where 1 ≤ k ≤ K and 1 ≤ n ≤ N.

D(k, n) can be computed by the following recurrence:

• D(1, n) = ∑_i=1..n (x_i - µ)², where µ = (∑_i=1..n x_i) / n

• D(k, n) = min_i=1..n-1 (D(k - 1, i) + ∑_j=i+1..n (x_j - (∑_t=i+1..n x_t) / (n - i))²)

Create a function k_mean_1D(K, L) that finds K optimal centroids for the list L. The function should return a pair containing the total distortion and the list of centroids.

Hint. Use dynamic programming.

Exercise 25.1 (convex hull GUI)

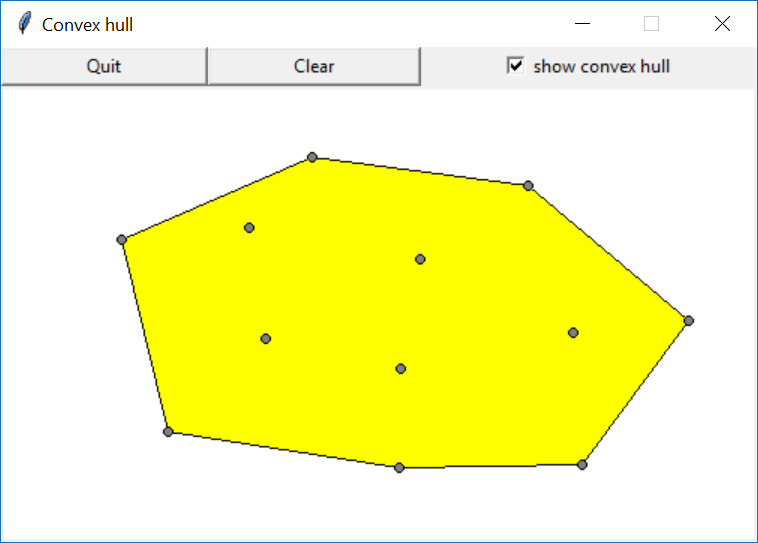
Create a Graphical User Interface (GUI) using the tkinter package to interactive create points and dynamically visualize the convex hull of the current point set. The GUI could e.g. consist of the following components:

1. A button 'Quit' to close the program

2. A button 'Clear' to remove all existing points

3. A checkbutton to enable/disable showing the convex hull of the current point set

4. A canvas showing the current set of points and the convex hull of the point set

5. Clicking on the canvas should create a new point

6. Clicking on an existing point should delete the point

Hint. See Handin 7 for the computation of the convex hull of a point set. Make a function redraw that redraws the content of the canvas, by first deleting all content of the canvas, and then plotting the points and the convex hull (if enabled) using the create_oval and create_polygon methods. The redraw method should be called whenever the canvas should be updated (new point, point deleted, all points deleted, and convex hull enabled/disabled). To capture clicks to the canvas apply the bind method of the canvas.

Exercise 26.1 (install Java)

Install the Java SE Development Kit (JDK). Remember to add the JDK folder containing javac, e.g. "C:\Program Files\Java\jdk-12.0.1\bin", to your path (see instructions from Java.com webpage).

Exercise 26.2 (hello world in Java)

Compile and run the following HelloWorld.java program:

public class HelloWorld {
    public static void main(String[] args) {
        System.out.println("Hello world");
    }
}

Exercise 26.3 (down payment in Java)

Implement Exercise 2.8 (down payment) in Java.

To read a double (64 bit floating point value) from the input you can use the following statement:

double loan = Double.parseDouble(System.console().readLine());

or using the java.util.Scanner class:

Scanner sc = new Scanner(System.in);
double loan = sc.nextDouble();

Exercise 27.1 (course evaluation)

Fill out the official course evalution.