Project I - Geometric medians

Motivation: Assume you want to build a drone tower from where to deliver parcels to costumers, and you know the destinations (points) where to deliver parcels. What is the optimal placement of the tower, if each drone can at most carry one parcel and needs to return to the tower between each delivery?

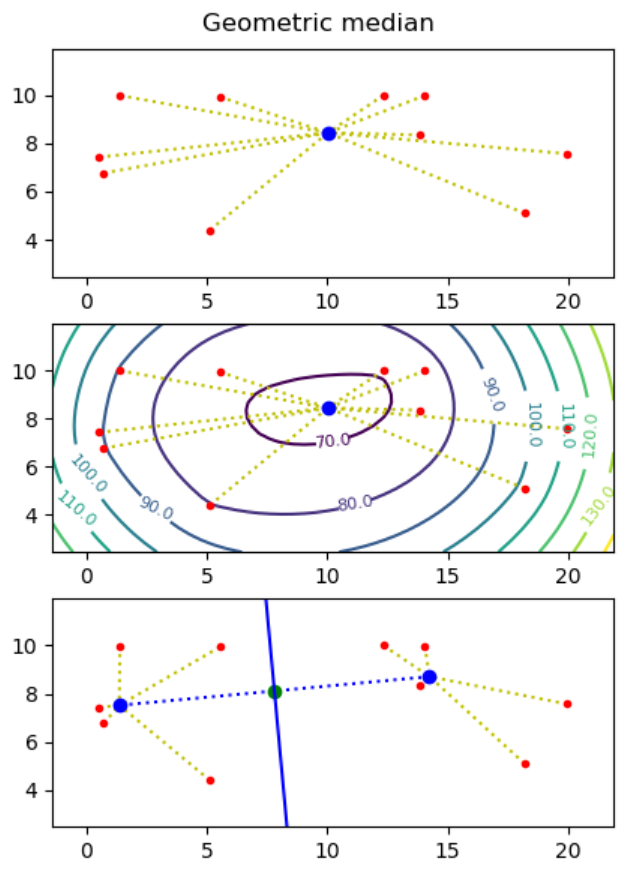
The geometric median of a point set S = {p₁, …, p_n} in the plane is a point q (not necessarily a point in S), that minimizes the sum of distances to the points, i.e. minimizes ∑_i=1..n |p_i - q|, where |p - q| = ((p_x - q_x)² + (p_y - q_y)²)^0.5.

1. Create a function geometric_median that given a list of points computes the geometric median of the point set.
   Hint. Use the minimize function from the module scipy.optimize.

2. Make representative visualizations that show both the input point sets and the computed geometric medians. Examples should include point sets with two and three points, and a random point set.

3. Use the matplotlib plotting function contour to plot a contour map to illustrate that it is the correct minimum that mas been found (the z-value for a point (x, y) in the contour map is the sum of the distances from (x, y) to all input points).

Next we want to find two points q₁ and q₂ such that the perpendicular bisector of q₁ and q₂ partitions the point set into the points closest to q₁ and those closest to q₂. We want to find two points q₁ and q₂ such that the sum of distances to the nearest point of q₁ and q₂ is minimized, i.e. ∑_i=1..n min(|p_i - q₁|, |p_i - q₂|) is minimized.

To solve this problem one essentially has to consider all possible bisection lines, and to find the geometric median on both sides of the bisector, e.g. using the algorithm from the first question. Assuming no three points are on a line, it is sufficient to consider all n(n-1)/2 bisector lines that go through two input points, and for each bisector line to consider the two cases where the two points on the line both are considered to be to the left or to the right of the line.

1. Create a function two_geometric_medians that give a list of points p₁, …, p_n computes two points q₁ and q₂ minimizing ∑_i=1..n min(|p_i - q₁|, |p_i - q₂|). It can be assumed that no three points are on a line.

2. Visualize your solution, showing imput points, q₁ and q₂, and the perpendicular bisector between q₁ and q₂.

3. Optional. Extend your solution to handle the case where three or more points can be on a line. E.g. what is your solution if you have four points on a line?